|
Question 1091713: 1)The senior classes at High School A and High School B planned separate trips to the local
amusement park. The senior class at High School A rented and filled 2 vans and 12 buses with 520
students. High School B rented and filled 13 vans and 3 buses with 230 students. Every van had the
same number of students in it as did the buses. How many students can a van carry? How many
students can a bus carry?
2)Sumalee's school is selling tickets to a spring musical. On the first day of ticket sales the school sold
6 adult tickets and 1 student ticket for a total of $23. The school took in $106 on the second day by
selling 12 adult tickets and 14 student tickets. Find the price of an adult ticket and the price of a
student ticket.
3)A boat traveled 60 miles downstream and back. The trip downstream took 3 hours. The trip back
took 6 hours. Find the speed of the boat in still water and the speed of the current.
4)The school that Carlos goes to is selling tickets to a choral performance. On the first day of ticket
sales the school sold 14 senior citizen tickets and 6 student tickets for a total of $180. The school
took in $117 on the second day by selling 12 senior citizen tickets and 1 student ticket. Find the
price of a senior citizen ticket and the price of a
Answer by ikleyn(52810)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The rule of this forum is ONE PROBLEM per post/ONE QUESTION per post.
So, I will solve only one problem for you.
3) A boat traveled 60 miles downstream and back. The trip downstream took 3 hours. The trip back
took 6 hours. Find the speed of the boat in still water and the speed of the current.
Let u be the boat speed in still water (in miles per hour, mph), and
let v be the current speed.
The effective speed of the boat moving downstream is 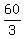 = 20 miles per hour.
This speed is the sum of the boat speed in still water and the current speed.
So, you have your first equation
u + v = 20 (1) for the effective speed downstream.
The effective speed of the boat moving upstream is = 20 miles per hour.
This speed is the sum of the boat speed in still water and the current speed.
So, you have your first equation
u + v = 20 (1) for the effective speed downstream.
The effective speed of the boat moving upstream is 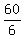 = 10 miles per hour.
This speed is the difference of the boat speed in still water and the current speed.
So, you have your second equation
u - v = 10 (2) for the effective speed upstream.
Thus you have this system of two equations in two unknowns
u + v = 20 (1)
u - v = 10 (2)
It is very special system, and it allows very special and very easy solution.
Add the two equations (1) and (2). You will get
2u = 20 + 10 = 30 ====> u = = 10 miles per hour.
This speed is the difference of the boat speed in still water and the current speed.
So, you have your second equation
u - v = 10 (2) for the effective speed upstream.
Thus you have this system of two equations in two unknowns
u + v = 20 (1)
u - v = 10 (2)
It is very special system, and it allows very special and very easy solution.
Add the two equations (1) and (2). You will get
2u = 20 + 10 = 30 ====> u =  = 15 mph.
Thus you just found the speed of the boat in still water It is 15 mph.
Then from (1), the current speed is v = 20 - u = 20 - 15 = 5 mph.
Answer. The speed of the boat in still water It is 15 mph.
The current speed is v = 20 - u = 20 - 15 = 5 mph. = 15 mph.
Thus you just found the speed of the boat in still water It is 15 mph.
Then from (1), the current speed is v = 20 - u = 20 - 15 = 5 mph.
Answer. The speed of the boat in still water It is 15 mph.
The current speed is v = 20 - u = 20 - 15 = 5 mph.
Solved.
You can check the solution on your own.
-------------
It is a typical and standard Upstream and Downstream round trip word problem.
You can find many similar fully solved problems on upstream and downstream round trips with detailed solutions in lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Wind and Current problems solvable by quadratic equations
- Unpowered raft floating downstream along a river
- Selected problems from the archive on the boat floating Upstream and Downstream
in this site.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
=============
Comment from student: Sorry, I wasnt sure about the amount of questions per post, thank you though.
My response. I can not accept such "Thank you" in the form "thank you though."
|
|
|
| |