|
Question 1091578: A student takes a true-false examination which contain of 10 questions.The student knows nothing about the subject and chooses answers at random.assuming independence between questions and probability of .9 of answering any question correctly,what is the probability that the student will pass the test(assume that passing means getting seven or more correct)? If the test contains 20 questions, the probability of passing change(14 or more correct)? plzzzzzzzzzz send complet solution
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the probability of getting the answer correct is .9
the probability of getting the answer wrong is therefore 1 - .9 = .1.
to get at least a 70% grade, then the student needs to answer at least 7 out of 10 or at least 14 out of 20.
7/10 = .7 = 70%
14/20 = .7 = 70%
to get at least 7 out of 10 correct, then 7 or 8 or 9 or 10 questions have to be answered correctly.
to get at least 14 out of 20 correct, then 14 or 15 or 16 or 17 or 18 or 19 or 20 have to be answered correctly.
the formula for x items correctly out of n items is:
p(x) = c(n,x) * p^x * q^(n-x)
when n = 10, the formula becomes:
p(7) = c(10,7) * .9^7 * .1^3
p(8) = c(10,8) * .9^8 * .1^2
p(9) = c(10,9) * .9^9 * .1^1
p(10) = c(10,10) * .9^10 * .1^0
you get a similar construction for at least 14 out of 20.
in that case, n = 20 and x = 14, 15, 16, 17, 18, 19, 20.
i used excel to do the math and this is what i got.
for at least 7 out of 10 possible occurrences:
probability is equal to .9872 or 98.72%
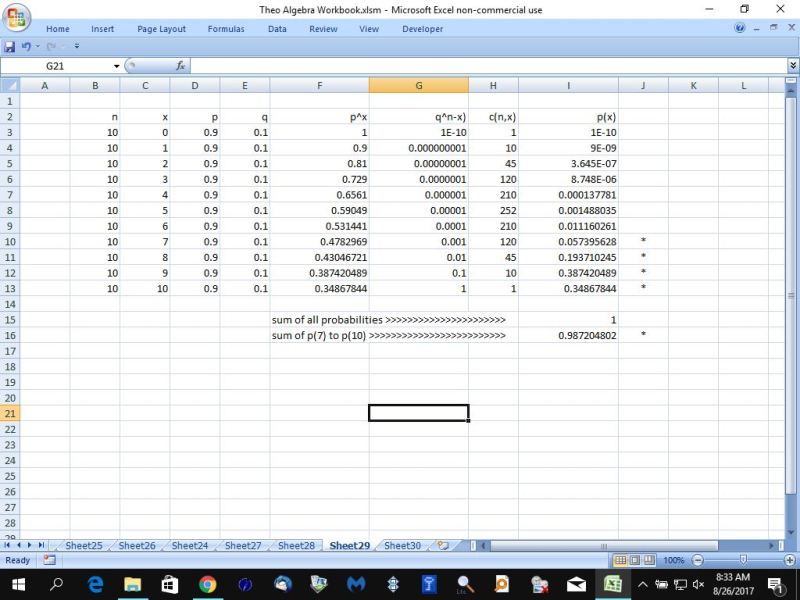
for at least 14 out of 20 possible occurrences:
probability is equal to.9976 or 99.76%

c(n,x) is the number of possible ways to get x out of n where order is not important.
that formula is c(n,x) = n! / (x! * (n-x)!)
for formula for the probability of x out of n is:
p(x) = c(n,x) * p^x * q^(n-x)
for example:
with 10 possible occurrences, the probability of getting exactly 7 out of 10 is:
p(7) = c(10,7) * .9^7 * .1^3 = .057395628
with 20 possible occurrences, the probability of getting exactly 17 out of 20 is:
p(17) = c(20,17) * .9^17 * .1^3 = .1901198714
both these calculations agree with what is shown in the excel spreadsheet.
the sum of all probabilities must be equal to 1.
the excel spreadsheet printouts show this to be true for both cases.
|
|
|
| |