SOLUTION: if a,b,c are in AP, aalnd a,mb,c are in GP then a, m^2b, c are in HP

If R,S,T are in AP, then S-R = T-S, or 

(1)  2S = R+T

If U,V,W are in GP, then 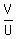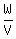, or 

(2)  UW = V2
 
If X,Y,Z are in HP, then their reciprocals are in AP, so

, 

Multiply through by LCD = XYZ

XZ-YZ = XY-XZ

(3)  2XZ = XY+YZ

Since a,b,c are in AP, then we substitute R=a, S=b, T=c in (1)

(4)  2b = a+c               <--we know this

Since  a, mb, c are in GP, then we substitute U=a, V=mb, W=c in (2)

(5)  ac = m2b2            <--we know this

We are to prove that a, m2b, c are in HP.  So to find 
out what we need to prove, we substitute X=a, Y=m2b, Z=c in (3)

(6)  2ac = am2b + m2bc    <--we are to prove this

So we will start with 2ac, and show that it is equal to am2b + m2bc

By (5),    

2ac = 2m2b2 

2ac = m2∙b∙2b, use (4) to substitute a+c for 2b 

2ac = m2∙b∙(a+c), distribute:

1ac = m2∙b∙a + m2∙b∙c

That's the same as

2ac = am2b + m2bc

which is (6), which is what we were to prove.

Edwin