Question 1091345: Your friend is saving pennies. She puts one penny into her piggy bank the first day, two pennies the second day, four the third day, and so on, doubling the number of pennies added. How many much money would she have at the end of vacation, if she could keep saving at this rate? Vacation lasts 75 days.
I would like to know if there is a formula for solving this problem, which I am fairly sure there is. I also have an understanding that the answer is very large.
Found 4 solutions by Boreal, mathmate, math_helper, MathTherapy:
Answer by Boreal(15235)   (Show Source): (Show Source):
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website! Question:
Your friend is saving pennies. She puts one penny into her piggy bank the first day, two pennies the second day, four the third day, and so on, doubling the number of pennies added. How many much money would she have at the end of vacation, if she could keep saving at this rate? Vacation lasts 75 days.
I would like to know if there is a formula for solving this problem, which I am fairly sure there is. I also have an understanding that the answer is very large.
Solution:
Indeed, the result is staggering.
She puts in one penny the first day, 2 pennies the second, 4 pennies the third, ...
The total sum is thus,
1, 3, 7, 15, 31, 63, 127, ...
Which translate to
2^1-1, 2^2-1, 2^3-1, 2^4-1, 2^5-1, 2^6-1, 2^7-1, ...
So at the end of the 75th day, the total amount is 2^75-1
or
37778931862957161709567 pennies
or
377,789,318,629,571,617,095.67 dollars
or
three hundred seventy-seven quintillion seven hundred eighty-nine quadrillion three hundred eighteen trillion six hundred twenty-nine billion five hundred seventy-one million six hundred seventeen thousand ninety-five dollars and sixty-seven cents
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! The answer is indeed huge:
Number Amount
of Days Saved (cents)
������ ������
1 1
2 3
3 7
4 15
5 31
: :
: :
n 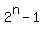
�
So after 75 days, she will have saved 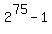 pennies, which is pennies, which is 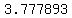 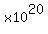 dollars� way, way, more money than is circulating in all the world's economies. dollars� way, way, more money than is circulating in all the world's economies.
�
To put that amount in perspective, it would be enough to pay off the entire national debt of the USA ($19,000,000,000,000), not just a few times, but over 19,883,000 times!
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your friend is saving pennies. She puts one penny into her piggy bank the first day, two pennies the second day, four the third day, and so on, doubling the number of pennies added. How many much money would she have at the end of vacation, if she could keep saving at this rate? Vacation lasts 75 days.
I would like to know if there is a formula for solving this problem, which I am fairly sure there is. I also have an understanding that the answer is very large.
Yes, there is! You need to use the formula for the sum of a GP, or a Geometric Sequence.
This is:  , with: , with:
 = Sum of "n" terms (Unknown, in this case) = Sum of "n" terms (Unknown, in this case)
 = Number of terms (75, in this case) = Number of terms (75, in this case)
 = First term (1, in this case) = First term (1, in this case)
 = Common Ratio (2, in this case) = Common Ratio (2, in this case)
Replacing all these variables should give you 
|
|
|