Let x = the lesser of two positive consecutive even integers.
Then x+2 = the greater of the two positive consecutive even
integers.
5 times lesser of two positive consecutive even integers
That's 5 times x, which is 5x
is at most...
That means "is less than or equal to",
written 
...four times the greater?
That's 4 times (x+2), which is written 4(x+2).
So altogether we now have:
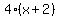and
What are the possible 4 pairs of positive consecutive even integers?
We solve the inequality:
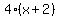Distribute to remove the parentheses on the right:
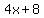Subtract 4x from both sides:
Since the lesser, x, must be even, x=2, x=4, x=6, or x=8
So there are 4 possibilities for x, namely, 2, 4, 6, and 8.
The four pairs of positive consecutive even integers
fulfilling the given requirements are:
{2,4}, {4,6}, {6,8}, {8,10}
Edwin
