Question 1091301: 13.The point P(–5, –12) is on the terminal arm of an angle in standard position.
a. Sketch the principal angle and label it. b. What is the measure of the related acute angle to the nearest degree?
c. What is the measure of theta to the nearest degree? d. What is the measure of the first negative co-terminal angle to the nearest degree?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the diagram i made of this problem is shown below.
look below the diagram for the words.
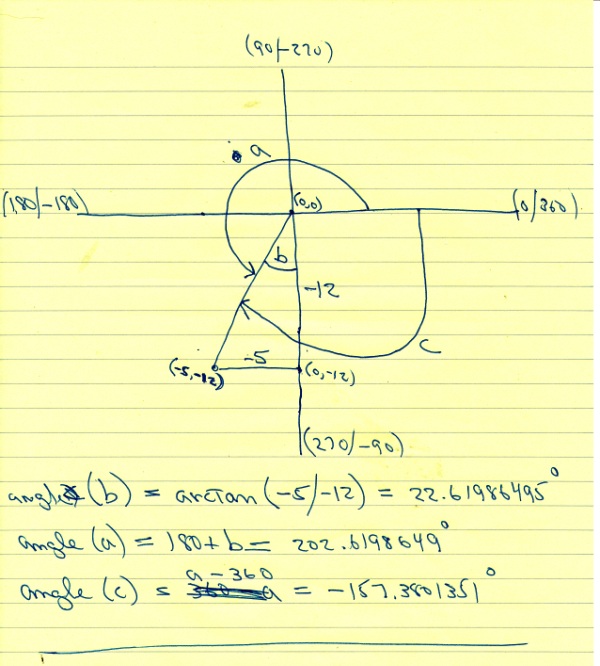
the center of the graph is at the point (0,0) which is the intersection of the horizontal axis and the vertical axis.
the 0 degree line is the horizontal line on the right side of the intersection.
this is also the 360 degree line if you are going in a counter clockwise direction fro the 0 degree line and the -360 degree line if you are going in a clockwise direction from the 0 degree line.
the vertical line on the top of the intersection is the 90 degree line if you are going in a counter-clockwise direction from the 0 degree line and is also the -270 degree line if you are going in a clockwise direction from the 0 degree line.
the horizontal line on the left side of the intersection is the 180 degree line if you are going in a counter clockwise direction from the 0 degree line and is also the -180 degree line if you are going in a clockwise direction from the 0 degree line.
the vertical line below the intersection is the 270 degree line if you are going in a counter clockwise direction from the 0 degree line and is also the -90 degree line if you are going in a clockwise direction from the 0 degree line.
positive angles go in a counter clockwise direction.
negative angles go in a clockwise direction.
the point (-5,-12) forms a right triangle.
the hypotenuse of this right triangle is the line between the point (-5,-12) and the center of the graph which is the point (0,0).
the altitude of this triangle is the line from the point (0,-12) and the point (0,0).
the base of this triangle is the line from the point (-5,12) and the point (0,-12).
the primary angle is the angle that goes in a clockwise direction from the 0 degree line to the line formed between the point (-5,-12) and the point (0,0).
that is labeled angle a.
before we can find that angle, we need to find the acute angle.
that is the angle that is formed inside the triangle between the line that is between (0,0) and (-5,-12) and the line between (0,0) and (0,-12).
that is labeled angle b.
to find angle b, you find the absolute value of the arctangent of (-5/-12).
that makes angle b equal to 22.61986495 degrees which you can round to 23 degrees.
angle a is equal to 180 plus angle b which makes angle b equal to 202.6198649 degrees which you can round to 203 degrees.
the equivalent negative angle is the angle formed in a clockwise direction from the 0 degree line and the line formed between (-5,-12) and (0,0).
that angle is labels as angle c.
that winds up being angle b minus 360 degrees which is equal to -157.3801351 degrees which you can round off to -157 degrees.
|
|
|