Question 1090926: I need help for this problem please.
Population y of one town x years after the year 2000 is modeled by the equation y=12053*1.0345^x
1. what was the population of the town in the year 2000?
2. equation for the population of the town as a continuous model?
3. the population is increasing or not? by what percent?
Thank you.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  where where
 = population of the town, and = population of the town, and
 = number of years after the year 2000. = number of years after the year 2000.
1. In the year 2000, 
 , because a non-zero number to the zero power is by definition equal to , because a non-zero number to the zero power is by definition equal to  . .
So, in the year 2000,
 . .
2.  is probably the expected/accepted answer, is probably the expected/accepted answer,
although  is a good approximation, is a good approximation,
and  is a valid answer. is a valid answer.
NOTE:
The teacher may not accept any true answer not fitting what was taught in class. That may include formulas, symbols, and formats that I can an only guess at. If you are asked to "show your work", you may be expected to start by writing a general "formula" for an exponential growth model, such as
 or or  (Letter symbols may vary). (Letter symbols may vary).
FURTHER EXPLANATION:
In this problem, the word "model" refers to a function/equation (such as as  ) that fits fairly well the data available, and may be a useful "model" to predict population growth in the near future, or estimate what the population was at a time there is no data for. ) that fits fairly well the data available, and may be a useful "model" to predict population growth in the near future, or estimate what the population was at a time there is no data for.
The word "continuous" refers to the fact although in real life the  and and  values jump from one integer to another, a function/equation used "as a continuous model" applies to any real value of values jump from one integer to another, a function/equation used "as a continuous model" applies to any real value of  , yields real values of , yields real values of  , and has a graph that is a curve flowing continuously through an infinite number of points, without any gaps. , and has a graph that is a curve flowing continuously through an infinite number of points, without any gaps.
With that understanding, I would say that  is one equation for the population of the town as a continuous model, but I believe that is not the expected answer. is one equation for the population of the town as a continuous model, but I believe that is not the expected answer.
For any number, equation, or function, there is a variety of representations limited only by your imagination. An exponential function can be written with any base, but in higher math the irrational number
 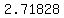 is a very popular base. is a very popular base.
Using base  logarithms of both sides of the equal sign in logarithms of both sides of the equal sign in  , ,
we can work our to an equivalent expression:







3. Of course the population is increasing.
On the year 2000,  and the population is and the population is  . .
One year later, the model predicts that for  that number will have multiplied times that number will have multiplied times 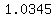 . .
That is  times more. times more.
It is  more in one year. more in one year.
The population is increasing by  per year. per year.
You may be expected to show by calculating the relative change
from  for for 
to  for for 
as  , ,
or you may be expected to apply a formula such as
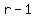 to find the percent increase as a decimal for to find the percent increase as a decimal for  . .
|
|
|