Question 1090691: ((x-3)/(x+2)) > 0
thanks anyone.
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
((x-3)/(x+2)) > 0
thanks anyone.
~~~~~~~~~~~~~~~~~
There are 2 critical points x= 3 and x= -2,
and there are 3 intervals ( , , ), (-2,3) and ( ), (-2,3) and ( , , ).
We consider all three intervals one after another, moving from the left to the right.
1. In the interval ( ).
We consider all three intervals one after another, moving from the left to the right.
1. In the interval ( , , ) the numerator (x-3) is negative; the denominator (x+2) is negative, too.
Hence, the ratio ) the numerator (x-3) is negative; the denominator (x+2) is negative, too.
Hence, the ratio 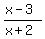 is positive.
2. In the interval (-2,3) the numerator (x-3) is negative; the denominator (x+2) is positive.
Hence, the ratio is positive.
2. In the interval (-2,3) the numerator (x-3) is negative; the denominator (x+2) is positive.
Hence, the ratio 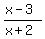 is negative.
3. In the interval ( is negative.
3. In the interval ( , , ) the numerator (x-3) is positive; the denominator (x+2) is positive, too.
Hence, the ratio ) the numerator (x-3) is positive; the denominator (x+2) is positive, too.
Hence, the ratio 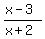 is positive.
4. Thus your answer is: The solution of the given inequality is this intervals union ( is positive.
4. Thus your answer is: The solution of the given inequality is this intervals union ( , , ) U ( ) U ( , , ). ).
Solved.
The plot is below. You can consider it as visual confirmation to the solution.

Plot y = 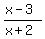
To see more solved problems/samples of this type, look into the lesson
- Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Inequalities".
|
|
|