Question 1090678: Which function describes exponential decay?
a.f(x)=6(1.01)^x c.f(x)=25(0.8)^x
b.f(x)=3.4(40)^2x d.f(x)=8(17)^a/4
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Multiple choice questions often require quick answers.
If you have the time, you can try for visualizing,
and achieving a deeper understanding.
When faced with such a question on a timed test, think smart (and fast).
A function that describes exponential decay
would be one that decreases as  increases. increases.
Obviously, with a base greater than  , ,
and no minus sign before the  in the exponent, in the exponent,
the functions
 , ,
 , and , and
 increase as increase as  increases. increases.
The only plausible answer is
 . .
Maybe you would recognize  as describing exponential decay, as describing exponential decay,
if I wrote it in an equivalent form.
 --> --> --> --> --> --> --> --> --> --> . .
Would you like to see  as the base of the exponential function? as the base of the exponential function?
 --> --> --> -->
  . .
Can you see why  decreases? decreases?
 , ,
 , ,
 , and , and
 . .
Can you see why  increases? increases?
 , ,
 , ,
 , ... , ...
You do not even need to calculate that far.
You must know that  , ,
 , ,
 , and , and
 are all exponential functions, are all exponential functions,
and you must know that exponential functions are monotonous,
meaning that they either increase all the way from  to to  , ,
or decrease all the way from  to to  . .
If you find that an exponential function where 
(or that  for some for some 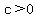 ), you know that the function increases throughout its domain. ), you know that the function increases throughout its domain.
|
|
|