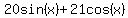 We draw a right triangle with legs having the lengths of those
two coefficients. We put the 20 on the adjacent side to y
and 21 on the opposite side, so that we can use the given
sin(x+y) formula. [If we did it the other way we'd have to
use the cos(x-y) formula.]
We draw a right triangle with legs having the lengths of those
two coefficients. We put the 20 on the adjacent side to y
and 21 on the opposite side, so that we can use the given
sin(x+y) formula. [If we did it the other way we'd have to
use the cos(x-y) formula.]
 Note here that y is the angle whose tangent is 21/20, and we
state that mathematically by the equation y = tan-1(21/20).
We calculate the hypotenuse by the Pythagorean theorem:
Note here that y is the angle whose tangent is 21/20, and we
state that mathematically by the equation y = tan-1(21/20).
We calculate the hypotenuse by the Pythagorean theorem:

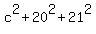




 We multiply the given expression, which is
We multiply the given expression, which is
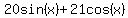 by
by 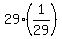 which is the same as multiplying
by 1, and does not change the value:
which is the same as multiplying
by 1, and does not change the value:
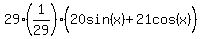 We distribute the
We distribute the 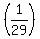
 We use the right triangle above to substitute trig
ratios for the fractions:
We use the right triangle above to substitute trig
ratios for the fractions:
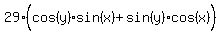 We rearrange the factors in the parentheses so that
what's inside the parentheses will look like the right
side of the given formula sin(x+y)=sin(x)cos(y)+sin(y)cos(x)
We rearrange the factors in the parentheses so that
what's inside the parentheses will look like the right
side of the given formula sin(x+y)=sin(x)cos(y)+sin(y)cos(x)
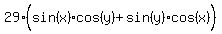 We replace the parentheses using the given formula:
We replace the parentheses using the given formula:
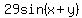 , where y = tan-1(21/20).
Edwin
, where y = tan-1(21/20).
Edwin