Question 1090340: Solve the inequality ((2x+5)(x-1)^2)/(x+2)^3 _> 0
if you could please thoroughly explain it because I am completely lost on this one.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) Write the inequality showing all the individual factors;
(2) Identify the critical points (where numerator or denominator is 0);
(3) Examine the function value in each of the intervals determined by the critical points to see whether the function value is positive or negative in that interval.
The given function is
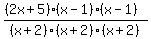
The factors in the numerator give you the values of x for which the function value is 0. Those x values are -2.5 and 1.
The factors in the denominator give you the values where the function is undefined, since division by 0 is not allowed. There is only one such value, x = -2.
The three critical values -2.5, -2, and 1 divide the domain into four intervals:
(-infinity, -2.5], [-2.5, -2), (-2,1], and [1,infinity]
Note that the notation I used there implies that -2.5 and 1 are zeros of the function, whereas -2 is an excluded value.
Now look at the signs of each of the six individual factors of the expression in each interval to determine the sign of the function in that interval.
(1) For x less than -2.5, the signs of all 6 factors are negative, so the function value is positive.
(2) For x between -2.5 and -2, the signs of 5 of the 6 factors are negative (the first factor in the numerator is now positive), so the function value is negative.
(3) For x between -2 and 1, the signs of only 2 of the 6 factors are negative (the three equal factors in the denominator are now positive), so the function value is again positive.
(4) For x greater than 1, all the signs are now positive, so the function value is positive.
So the only interval on which the function value is negative is between -2.5 and -2. The problem asks for the solution set for when the value of the expression is greater than or equal to zero. That solution set is the first, third, and fourth intervals determined by the critical points:
(-infinity, -2.5], (-2,1], and [1,infinity]
or just
(-infinity, -2.5] and [-2,infinity]
Note that, with a little experience with this type of problem, you can determine where the function value is positive or negative with less effort than described above. To do this, we imagine walking along the x axis from negative infinity to positive infinity, and we watch for where the sign of the function changes. Note that the sign can change only at the critical values of the function.
For this example, the analysis would go like this:
For x values less than -2.5, all 6 factors are negative, so the function value is positive.
When we pass x=-2.5, the sign of one factor changes, so the sign of the function changes; it is now negative.
When we pass x=-2, the signs of three factors change, so the sign of the function changes again; it is now positive.
When we pass x=1, the signs of the last two factors change sign, so the sign of the function does NOT change; it is still positive.
|
|
|