Question 1090326: Approximate, to the nearest 10l, the solutions of the equation that are in
[0c, 360c).
sec q = -1.116
I don't knoq what to do. Please help!
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! What did you mean by "to the nearest 10l" ?
Was it a typo and you meant to the nearest  ?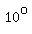
Are you allowed to use a calculator?
I believe you are asking for solutions to 
in the interval      .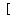
The interval 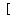is the values between (included) and (not included),
so you are looking for solutions with  .
The trigonometric function is secant, which is the reciprocal of cosine, meaning
 .
The graph of the function  ,
with  measured in degrees looks like the red curve below:
 .
The graph of the function  ,
with measured in degrees looks like the red curve below:
 .
The solutions to
in the interval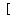
are the values for the two circled points marked below
 .
Those two points are the only points on the graph with 
and between and .
Finding solutions:
  .
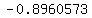Using the function inverse cosine in a calculator you can find
the solution for  that is between and  ,
(the second quadrant solution):
  .
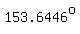So,  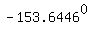is third quadrant solution,
but if we want one between and ,
we need to add , to get
 .
|
|
|
