SOLUTION: factor (1)/(x^(2))-(1)/(x)=6

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: factor (1)/(x^(2))-(1)/(x)=6      Log On


   

Question 1090261: factor (1)/(x^(2))-(1)/(x)=6
Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.
factor (1)/(x^(2))-(1)/(x)=6
~~~~~~~~~~~~~~~~~ 

Introduce new variable  y = 1%2Fx.      (1)


Then your equation will take the form

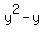y%5E2+-+y = 6,    or, equivalently,

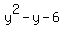y%5E2+-+y+-+6 = 0.          (2)

The left side quadratic polynomial can be easily factored 

(y-3)*(y+2) = 0.      (3)


It gives the roots of the equation  y = 3  and  y = -2.


Let us consider both cases.


1.  If y = 3,   then  x = 1%2Fy = 1%2F3,  due to (1).


2.  If y = -2,  then x = 1%2Fy = -1%2F2.


Answer.  The original equation has the roots  1%2F3  and  -1%2F2.

Solved.


Notice.  The formulation of the problem in your post is not exactly adequate.

The ideally balanced formulation is  THIS: 

     Solve the equation  (1)/(x^(2))-(1)/(x)=6  using factoring.