Question 1090083: The polynomial $f(x)$ has degree 3. If $f(-1) = 15$, $f(0)= 0$, $f(1) = -5$, and $f(2) = 12$, then what are the $x$-intercepts of the graph of $f$? Please explain your work thoroughly so I can understand. Thanks!
Answer by ikleyn(52807)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let f(x) = ax^3 + bx^2 + cx + d with unknown coefficients a, b, c and d.
Since f(0) = 0, it implies d = 0 (to see it, simply substitute x= 0 into the polynomial).
So, you need to determine a, b and c.
f(-1) = 15 ====> -a + b - c = 15, (1)
f(1) = -5 ====> a + b + c = -5, (2)
f(2) = 12 ====> 8a + 4b + 2c = 12. (3)
Add equations (1) and (2). You will get 2b = 15 + (-5) = 10 ====> b = 5.
Then equations (2) and (3) take the form
a + 5 + c = -5 (4) (instead of (2))
8a + 4*5 + 2c = 12 (5) (instead of (3))
or, which is the same
a + c = -10, (4')
4a + c = -4, (5')
Subtract (4') from (5') to get 3a = 6, a = 2.
Then from (4') c = -12.
Thus the polynomial is f(x) =  = = 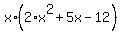 = (factor ! ) = = (factor ! ) = 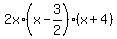 = = 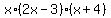 .
Thus the x-intercepts are .
Thus the x-intercepts are  , 0 (given !) and -4. , 0 (given !) and -4.
Solved.
|
|
|