Question 1089943: if the perimeter of a rhombus is 40 cm and one of its diagonals is 12cm, find the other diagonal
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
1. Since the sides of each rhombus have the same measures, the side length is  of the perimeter, i.e. 10 cm.
2. In each rhombus, diagonals divide it in four congruent right-angled triangles.
As we just found, the hypotenuse of each such triangle is 10 cm.
One leg of each such triangle is half of the diagonal of 12 cm long, i.e. has the length of 6 cm.
3. Thus we have a right-angled triangle with the hypotenuse of 10 cm and one leg of 6 cm.
Hence, the other leg is 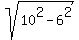 = 8 cm long.
4. Then the length of the other diagonal of the rhombus is twice 8 cm, i.e. 16 cm.
Answer. The other diagonal is 16 cm long.
Solved.
On properties of rhombis, see the lesson
- Diagonals of a rhombus are perpendicular
- Diagonals of a rhombus bisect its angles
in this site.
Also, you have this free of charge online textbook on Geometry
GEOMETRY - YOUR ONLINE TEXTBOOK
in this site.
The referred lessons are the part of this textbook under the topic "Properties of rhombis".
Answer by MathLover1(20849)  (Show Source):
|
|
|
