|
Question 1089899: Find the domain:
Y= sqrt. tan(x)
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Because of the periodic nature of tan(x), this is a tough one.
When finding domains one looks for things that are undefined in the set of Real numbers. Among the things to avoid are:- Zeros in denominators
- Negative radicands of even-numbered roots. For example:
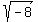 - Zero or negative arguments to logarithm functions
Your expression has two of these:- A denominator. It is hidden in the tan function! Since
 we cannot allow x values which make cos(x) be zero! we cannot allow x values which make cos(x) be zero!
cos(x) = 0 when x =  , , 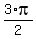 , , 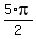 , etc. So we must exclude all these values from the domain. , etc. So we must exclude all these values from the domain. - An even-numbered root: square root. So we cannot allow tan(x) to be negative.
tan(x) < 0 when 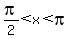 , , 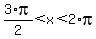 , , 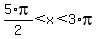 , .etc. , .etc.
The domain is rest of the Real numbers:  , ,  , ,  , ,  , etc. Expressing this succinctly and completely is not easy. The domain is: , etc. Expressing this succinctly and completely is not easy. The domain is:
{  } where n is any integer. } where n is any integer.
Think about various integers. Subsitute them in for n above and see if you can recognize that you get one of the intervals listed or suggested by the "etc." list above.
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The correct answer is
The domain of the given function is the union of all semi-intervals 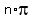 <= x < <= x < 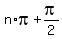 , for all integer n.
Each semi-interval includes its left endpoint and excludes its right endpoint. , for all integer n.
Each semi-interval includes its left endpoint and excludes its right endpoint.
|
|
|
| |