`
WARNING: FOMBITZ' SOLUTION IS INCORRECT.
CORRECT SOLUTION BY EDWIN:
Solve each of the following systems by graphing.
x - 2y = 8
3x - 2y = 12
Get two points on the first line.
Plot them and draw a line through them.
Get two points on the second line.
Plot them and draw a line through them.
Identify the coodinates of the point where the two lines cross.
Get two points on the first line whose equation is x - 2y = 8
Arbitrarily pick any convenient number to substitute
for either letter. I think I will first choose 0 to substitute
for x. I chose 0 simply because it is easy. I could have chosen
any other number, and for either letter. So we substitute x = 0
x - 2y = 8
0 - 2y = 8
-2y = 8
y =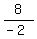 
y = -4, so one point on the first line is (x, y) = (0,-4)
Now for the second point on the first line, I think I will choose 0 to substitute for y. Again I chose 0 simply because it is easy. I could
have chosen any other number, and for either letter. So we substitute
y = 0
x - 2y = 8
x - 2(0) = 8
x - 0 = 8
x = 8, so another point on the first line is (x, y) = (8, 0)
Plot the two points (0, -4) and (8, 0):
Draw a straight line through them:
Get two points on the second line, whose equation is 3x - 2y = 12
Arbitrarily pick any convenient number to substitute
for either letter. I will again first choose 0 to substitute
for x. Again I chose 0 simply because it is easy. I could have chosen
any other number, and for either letter. So we substitute x = 0
3x - 2y = 12
3(0) - 2y = 12
-2y = 12
y =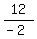 
y = -6, so one point on the second line is (x, y) = (0,-6)
Now for the second point on the second line, I will again choose 0 to
substitute for y. Again I chose 0 simply because it is easy. I could
have chosen any other number, and for either letter. So we substitute
y = 0
3x - 2y = 12
3x - 2(0) = 12
3x - 0 = 12
3x = 12
x = 
x = 4
so another point on the second line is (x, y) = (4, 0)
Plot the two points (0, -6) and (4, 0):
Draw a straight line through them:
To identify the coodinates of the point where the
two lines cross, draw both a horizontal line and
a vertical line through that point. These are the
green lines below:
Notice that the vertical green line goes through 2 on
the x-axis, and the horizontal one goes through -3 on
the y-axis, so the solution is
(x, y) = (2,-3)
We now check to see if we are correct.
First we substitute x = 2, and y = -3 into the first
equation to see if we get a true statement:
x - 2y = 8
2 - 2(-3) = 8
2 + 6 = 8
8 = 8
That is true, but to completely check the problem
we must also substitute x = 2, and y = -3 into the second
equation to see if we also get a true statement.
3x - 2y = 12
3(2) - 2(-3) = 8
6 + 6 = 12
12 = 12
That is true also, so (x, y) = (2, -3) is the correct
solution to the system.
Edwin
