SOLUTION: Solve each of the following systems by graphing. 2x-y=4 2x-y=6

Solve each of the following systems by graphing.

2x - y = 4
2x - y = 6

Get two points on the first line.
Plot them and draw a line through them.
Get two points on the second line.
Plot them and draw a line through them.
Identify the coodinates of the point where the two lines cross.

Get two points on the first line whose equation is  2x - y = 4

Arbitrarily pick any convenient number to substitute
for either letter.  I think I will first choose 0 to substitute
for x.  I chose 0 simply because it is easy.  I could have chosen
any other number, and for either letter.  So we substitute x = 0

  2x - y = 4
2(0) - y = 4
   0 - y = 4
      -y = 4
     -1y = 4
      y =  
      y = -4, so one point on the first line is (x, y) = (0,-4) 

Now for the second point on the first line, I think I will choose 0 to substitute for y.  Again I chose 0 simply because it is easy.  I could 
have chosen any other number, and for either letter.  So we substitute
y = 0

  2x - y = 4
 2x -(0) = 4
      2x = 4
       x = 
       x = 2, so another point on the first line is (x, y) = (2, 0)

Plot the two points (0, -4) and (2, 0):

 

Draw a straight line through them:

 

Get two points on the second line, whose equation is 2x - y = 6

Arbitrarily pick any convenient number to substitute
for either letter.  I will again first choose 0 to substitute
for x.  Again I chose 0 simply because it is easy.  I could have chosen
any other number, and for either letter.  So we substitute x = 0

  2x - y = 6
2(0) - y = 6
      -y = 6
       y =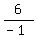 
       y = -6, so another point on the second line is (x, y) = (0, -6) 

Now for the second point on the second line, I will again choose 0 to
substitute for y.  Again I chose 0 simply because it is easy.  I could 
have chosen any other number, and for either letter.  So we substitute
y = 0

  2x - y = 6
 2x -(0) = 6
      2x = 6
       x =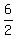 
       x = 3, so another point on the first line is (x, y) = (3, 0)

Plot the two points (0, -4) and (3, 0):

so another point on the second line is (x, y) = (4, 0)

Plot the two points (0, -6) and (3, 0):

 

Draw a straight line through them:

 

Oh,oh!  These two lines are parallel and therefore
they do not intersect, so there is no solution.

This type of system is called "inconsistent".

Edwin