Question 108981This question is from textbook
: graph including any oblique asymptotes (x^2+5)/(x+1). I know how to graph it in a calculator. this problem is one found on pg 300 matched problem 6. I am not understanding how to do this problem based of the example given to me on the previous page. I have the answer in the book. it is all done on a gragh but I don't understand how to mathmatically work this out I can do it on a calculator but I need to know how to show this with out a calculator.
This question is from textbook
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! Let's do some analysis.
When you look at the function,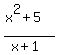 and you're interested in asymptotes, you need to ask a couple of questions.
1. When does the denominator go to zero?
2. What happens when x gets very large in the positive direction?
3. What happens when x gets very large in the negative direction?
Let's look at each question.
1. The denominator goes to zero at x=-1.
So at x=-1, your function is undefined.
Just to the right of it, the function goes near positive infinity (x+1>0).
Just to the left of it, the function goes near negative infinity (x+1<0).
So at x=-1, you have a vertical asymptote.
2. As x gets very large positively,
So for very large x, the function looks like y=x.
As an example, at x=100,
So you have another asymptote that looks like the function y=x.
3. As x gets very large negatively,
So for very large x, the function also looks like y=x for large positive x
As an example, at x=-100,
So you have another asymptote that looks like the function y=x for large negative x.
But it all together and you can graph the function.
|
|
|
