SOLUTION: If x^2 + y^2 =2 and xy = 1, find x^2-y^2

If  

x^2 + y^2 =2      (1)    and 
xy = 1,           (2)

then  x = ,   =  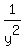 and, after substituting it into (1), you get this equation for the single unknown y

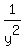 +  = 2,    which is the same as

 - 2 + 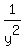 = 0,   or

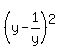 = 0,   which implies

y = 1/y   and then   y^2 = 1;  finally,   y = 1   OR  y= -1.


If y = 1, then, obviously x = +/-1;   If y = -1, then, again, x = +/-1.


Taking into account that xy = 1, you can conclude that the solutions to (1),(2) are these two pairs (two points):  (1,1)   and   (-1,-1).


And you can easily check that in both cases   -  = 0.


Answer.  If x^2 + y^2 =2 and xy = 1,  then  x^2-y^2 = 0.