Question 1089475: The first four terms of gp is 30 and that of the last four term is 960 if the first term of gp is 1 find common ratio
Answer by ikleyn(52795)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The  first four terms of gp is 30 and that of the last four term is 960 if the first term of gp is 1 find common ratio. first four terms of gp is 30 and that of the last four term is 960 if the first term of gp is 1 find common ratio.
~~~~~~~~~~~~~~~~~~~
If the first term is 1, then from the first part of the condition we have
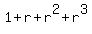 = 30. (1)
I don't know how to solve it analytically for r (if do not use the Cardano's formula, which is, obviously, not from this opera).
See the plot = 30. (1)
I don't know how to solve it analytically for r (if do not use the Cardano's formula, which is, obviously, not from this opera).
See the plot
 Plot y =
Plot y = 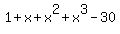 I created a table in Excel, which shows that r is between 2.67 and 2.68,
but it is clear that the graphical method (or any approximate "technology" method)
is not what is expected as the solution method for this problem.
The second condition does not give much:
it gives the second equation
I created a table in Excel, which shows that r is between 2.67 and 2.68,
but it is clear that the graphical method (or any approximate "technology" method)
is not what is expected as the solution method for this problem.
The second condition does not give much:
it gives the second equation
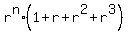 = 960, (2)
with some unknown "n", which combined with (1) gives = 960, (2)
with some unknown "n", which combined with (1) gives 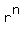 = =  = 32.
but the condition does not give any clue for the value of n.
So, although the "technology" can provide some approximate solution,
looking into the problem "in large", I don't think that the condition is correct.
Again:
the problem (as it is presented in the post) is reduced to two equations in two unknowns r and n = 32.
but the condition does not give any clue for the value of n.
So, although the "technology" can provide some approximate solution,
looking into the problem "in large", I don't think that the condition is correct.
Again:
the problem (as it is presented in the post) is reduced to two equations in two unknowns r and n
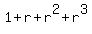 = 30, (1) and = 30, (1) and
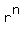 = 32, (2)
and I don't want (and don't know how) to go further.
It doesn't look to be attractive. = 32, (2)
and I don't want (and don't know how) to go further.
It doesn't look to be attractive.
--------------------
I thought one step further, and I am 170% sure that the presented formulation is incorrect.
Indeed, from the plot (and from my Excel table) I just have the correct estimation for r ~ 2.67 -:- 2.68.
Next, from equation (2) I have 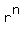 = 32 for some n. = 32 for some n.
Now, 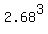 = 19.25, while = 19.25, while  = 51.59. = 51.59.
Hence, such integer positive "n" satisfying (1) and (2), simply DOES NOT EXIST.
In conclusion, let me say THIS:
It is VERY DIRTY BUSINESS to post incorrect problems to the forum.
It costed me about 2 hours of my time, which I spent for NOTHING.
|
|
|