Question 1089390: Skidding Car: The force needed to keep a car from skidding on a curve varies inversely as the radius r of the curve and jointly as the weight of the car and the square of the speed. It takes 3000 lb of force to keep a 200 lb car from skidding on a curve of radius 500 ft at 30 mph. What force will keep the same car from skidding on a curve of radius 800 ft at 60 mph?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = force needed to keep a car from skidding, in lb of force = force needed to keep a car from skidding, in lb of force
 = radius of the curve, in feet = radius of the curve, in feet
 = speed of the car, in mph = speed of the car, in mph
We could make
 = weight of the car, but that does not change. = weight of the car, but that does not change.
For inverse and direct variations there is always a constant,
multiplied times the variables involved in direct variation,
and divided by the variables involved in inverse variation.
In this case the relation of  with the variables is with the variables is

As it is the same car,  is constant, so we can write it simply as is constant, so we can write it simply as
 (with a new constant (with a new constant  ). ).
We are told that  for for  and and  , so , so




So, the relation is
 . .
When the speed is  and the radius is and the radius is  , ,



 . .
The force needed to keep a car from skidding when taking a curve
with radius 800 ft at 60 mph is 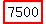 lb of force. lb of force.
|
|
|