SOLUTION: The graph of 2y^4 -x^2 +11 =0 is symmetric with respect which of the following? 1. The x axis 2. The y axis 3. The origin A)only 1 B)only 2 C)only 3 D)1,2, and 3

Click here to see ALL problems on Finance

Question 1089223: The graph of 2y^4 -x^2 +11 =0 is symmetric with respect which of the following?
1. The x axis
2. The y axis
3. The origin
A)only 1
B)only 2
C)only 3
D)1,2, and 3
Found 2 solutions by rothauserc, ikleyn:
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website!
2y^4 -x^2 +11 = 0
:
y = f(x) = (x^2 -11)^(1/4) / 2^(1/4)
:
f(-x) = f(x)
symmetric with respect to the y axis
this is an even function
:
***********
Answer is B
***********
:

Answer by ikleyn(52835)   (Show Source):
You can put this solution on YOUR website!
.

The graph of 2y^4 -x^2 +11 =0 is symmetric with respect which of the following? 1. The x axis 2. The y axis 3. The origin A) only 1 B) only 2 C) only 3 D) 1, 2, and 3 Plot y1 = (red) and y2 = 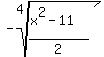(green).

      The correct answer is OPTION D).

0. Let the point (x,y) belongs to the curve. It means that its coordinates satisfy the equation 2y^4 -x^2 +11 =0. (1) 1. Then the point (-x,y) also belongs to the curve. Indeed, then 2y^4 - (-x)^2 + 11 = 2y^4 - x^2 + 11 = 0 due to (1). It means that the symmetry (x,y) --> (-x,y) relative to the axis "Y" is in place. 2. Also, then the point (x,-y) belongs to the curve. Indeed, then 2(-y)^4 - x^2 + 11 = 2y^4 - x^2 + 11 = 0 due to (1). It means that the symmetry (x,y) --> (x,-y) relative to the axis "X" is in place. 3. Finally, then the point (-x,-y) belongs to the curve. Indeed, then 2(-y)^4 - (-x)^2 + 11 = 2y^4 - x^2 + 11 = 0 due to (1). It means that the symmetry (x,y) --> (-x,-y) relative to the origin is in place.

Thus my statement is PROVED and the solution is COMPLETED.

        Proved.   Solved.   And completed.

The other's tutor solution is   WRONG   (his approach is   WRONG   and his answer is   UNCOMPLETED).