Question 1089204: In triangle ABC, the value of acotA+bcotB+ccotC is?
a)R+r
b)(R+r)/R
c)2(R+r)
d)3(R+r)
Also explain how?
Answer by ikleyn(52887)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In triangle ABC, the value of acotA+bcotB+ccotC is?
a)R+r
b)(R+r)/R
c)2(R+r)
d)3(R+r)
Also explain how?
~~~~~~~~~~~~~~~~~~~
It requires two ideas.
1. a*cot(A) + b*cot(B) + c*cot(C) = 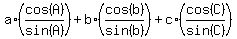 = = 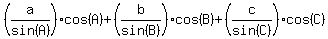 . (1)
Next, . (1)
Next, 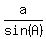 = 2R, = 2R, 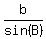 = 2R and = 2R and 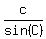 = 2R, where R is the radius of the circumscribed circle around the triangle,
according to the Sine Law theorem (see the lessons Law of sines and Law of sines - the Geometric Proof in this site).
Therefore, the line (1) can be continued in this way
a*cot(A) + b*cot(B) + c*cot(C) = 2R*(sin(A) + sin(B) + sin(C)). (2)
It is the first idea, and it allows us to reduce the problem to calculation of sin(A) + sin(B) + sin(C).
2. The second idea is THIS:
For any triangle with angles A, B and C
sin(A) + sin(B) + sin(C) = = 2R, where R is the radius of the circumscribed circle around the triangle,
according to the Sine Law theorem (see the lessons Law of sines and Law of sines - the Geometric Proof in this site).
Therefore, the line (1) can be continued in this way
a*cot(A) + b*cot(B) + c*cot(C) = 2R*(sin(A) + sin(B) + sin(C)). (2)
It is the first idea, and it allows us to reduce the problem to calculation of sin(A) + sin(B) + sin(C).
2. The second idea is THIS:
For any triangle with angles A, B and C
sin(A) + sin(B) + sin(C) = 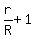 , (3)
where r is the radius of the inscribed circle, while R is the radius of the circumscribed circle about the triangle.
Deriving formula (3) requires some technique, but it is known proof, which you can find at this reference
https://math.stackexchange.com/questions/734395/how-to-prove-that-fracrr1-cos-a-cos-b-cos-c
3. Finally, a*cot(A) + b*cot(B) + c*cot(C) = 2R*(r/R + 1)}}} = 2*(R+r). , (3)
where r is the radius of the inscribed circle, while R is the radius of the circumscribed circle about the triangle.
Deriving formula (3) requires some technique, but it is known proof, which you can find at this reference
https://math.stackexchange.com/questions/734395/how-to-prove-that-fracrr1-cos-a-cos-b-cos-c
3. Finally, a*cot(A) + b*cot(B) + c*cot(C) = 2R*(r/R + 1)}}} = 2*(R+r).
Solved.
|
|
|