Question 1089163: convert the equation to standard for by completing the square on x. Then find the vertex, focus and directrix of the parabola. then graph
x^2+2x-8y-31=0
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The "vertex" form of a parabola with its vertex at ( , , ) is: ) is:
regular: 
sideways: 
The conics form of the parabola equation (the one you'll find in advanced or older texts) is:
regular: 
sideways: 
where the value of 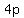 is actually the same as the value of is actually the same as the value of 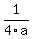
 ....since coefficients ....since coefficients  and and  , we have , we have  -> -> -> ->



 => =>  and and  , and , and
the vertex is at ( , , ) )
The focus is "p" units from the vertex:
 , ,
so 
then,
the focus is  unit above the vertex, at ( unit above the vertex, at ( , ,  ), ),
and the directrix is the horizontal line , p or , p or  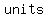 below the vertex below the vertex

|
|
|