SOLUTION: Find the sum of n term of the series. 1+4+13+40+........ .

Algebra ->  Finance -> SOLUTION: Find the sum of n term of the series. 1+4+13+40+........ .      Log On


   

Question 1089104: Find the sum of n term of the series.
1+4+13+40+........ .
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
If you calculate the differences between consecutive terms,
you find that those differences form a geometric sequence
(or geometric progression, or GP, if those are the preferred names where you live).
The terms are
a%5B1%5D=1=3%5E0 ,
a%5B2%5D=a%5B1%5D%2B3%5E1=1%2B3=4 ,
a%5B3%5D=a%5B2%5D%2B3%5E2=4%2B9=13 ,
a%5B4%5D=a%5B3%5D%2B3%5E3=13%2B27=40 .
So, a%5Bn%5D=1%2B3%2B3%5E2%2B3%5E3%2B%22...%22%2B3%5E%28n-1%29
The differences form a geometric sequence/progression with common ratio r=3.
So, you can calculate each term as the sum of that geometric sequence/progression.
You can also figure it out from polynomial products,
knowing that %28x-1%29%2A%281%2Bx%2Bx%5E2%2Bx%5E3%2B%22...%22%2Bx%5E%28n-1%29%29=x%5En-1 ,
and for x=3 you have
%283-1%29%2A%281%2B3%2B3%5E2%2B3%5E3%2B%22...%22%2B3%5E%28n-1%29%29=3%5En-1 .
Either way, you end up with
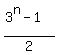
a%5Bn%5D=sum%283%5Ek%2Ck=0%2Cn-1%29%22=%22%283%5En-1%29%2F%283-1%29%22=%22%283%5En-1%29%2F2
Each term is the sum of all the terms before,
The sum of you have to calculate is
1%2B4%2B13%2B40%2B%22...%22%2Ba%5Bn%5D=sum%28a%5Bk%5D%2Ck=1%2Cn%29%22=%22
.
The sum in the formula is related to the one we had calculated before:
, so
1%2B4%2B13%2B40%2B%22...%22%2Ba%5Bn%5D=%281%2F2%29%283%283%5En-1%29%2F2%29-n%2F2%22=%223%283%5En-1%29%2F4-n%2F2