Question 1088858: If x+2 is a factor of x^3 - ax- 6,then find the remainder when 2x^3+ax^2-6x+9 is divided by x+1.
Please help me with this question.
Thank You.
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! If x+2 is a factor of x^3 - ax- 6,then find the remainder when 2x^3+ax^2-6x+9 is divided by x+1.
Please help me with this question.
Thank You.
Solving this by substituting 0 for f(- 2), and - 2 for x, you will get a = 7.
Since x + 1 is a factor, then a zero is - 1. You now need to use either POLYNOMIAL LONG DIVISION to DIVIDE 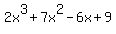 by x + 1, or synthetic division to determine the remainder.
IGNORE the rubbish the other person POSTED. You'll only CONFUSE yourself a great deal if you decide to follow him. Most people already know this. Be FOREWARNED!!
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
If x+2 is a factor of x^3 - ax- 6,then find the remainder when 2x^3+ax^2-6x+9 is divided by x+1.
Please help me with this question.
Thank You.
~~~~~~~~~~~~~~~~~
Let me do it in a way in how it SHOULD BE DONE.
1. If (x+2) is a factor of 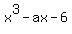 , then, according to the Remainder theorem, the number -2 is the root of the polynomial p(x) = .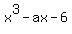
In other words, p(-2) = 0, which means
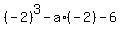 = 0, or, simplifying,
-8 + 2a - 6 = 0, or 2a = 8 + 6 = 14 ====> a =  = 7.
3. Hence, the second polynomial is
q(x) = .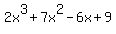
Then, again, due to the Remainder theorem, the remainder of division q(x) by (x+1) is equal to the value q(-1), i.e.
q(-1) = 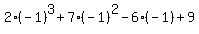 = 2*(-1) + 7*1 + 6 + 9 = 20.
Answer. The remainder of division the second polynomial by (x+1) is 20.
Solved.
---------------
The remainder theorem:
1. The remainder of division the polynomial  by the binomial  is equal to the value  of the polynomial.
2. The binomial divides the polynomial if and only if the value of  is the root of the polynomial , i.e.  .
3. The binomial factors the polynomial if and only if the value of is the root of the polynomial , i.e. .
See the lesson
- Divisibility of polynomial f(x) by binomial (x-a) and the Remainder theorem
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Divisibility of polynomial f(x) by binomial (x-a). The Remainder theorem".
--------------
Ignore writing by @josgarithmetic. His way IS NOT the method for solving such problems.
It is not his level of knowledge and is not his area of expertise.
|
|
|
