SOLUTION: sketch each system of equations. Then solve the system by the substitution method x^2 + y^2=6 y=x^2

 = 6,     (1)
y = .        (2)





Plots  = 6   and  y = .



To solve the system, replace  in the equation (1) by y, according to (1). You will get

y + y^2 = 6,         (3)   or

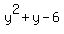 = 0,         (4)

(y+3)*(y-2) = 0  ====>  the roots are  = -3  and   = 2.


Since y = ,  y must be positive, so only the root y = 2 survives.


Then x = +/- .


Answer. The solutions to the system  (1),(2)  are  (x,y) = (,)  and  (x,y) = (,).