Question 1088728: Find the principal needed now to get the given amount; that is, find the present value.
To get $3000 after 33/4 years at 5% compounded daily.
The present value of $ 3000 is?$______
(Round to the nearest cent as needed.)
Found 2 solutions by Theo, MathTherapy:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! f = p * (1+r) ^ n
f = 3000
p = what you want to find.
r = 5% / 365 / 100 = .0001369863014
n = 33 * 365 = 12045
number of days in a year can be 360, 365, 365.4, or some other value depending on how you look at the number of days in a year.
i chose 365.
if the number of days in a year is different than that, you can redo the calculations using the other value for number of days in a year.
interest rate = interest rate % divided by 100.
formula becomes:
3000 = p * (1 + .0001369863014) ^ 12045
simplify to get:
3000 = p * 5.206391456
solve for p to get:
p = 3000 / 5.206391456 = 576.2148362
an investment of 576.2148362 will becomes 3000 in 33 years at 5% compounded daily.
576.2148362 * (1 + 1.369863014 * 10 ^ -4) ^ (33 * 365) = 3000
note that 1.369863014 * 10 ^ -4 is equal to .0001369863014
note that 33 * 365 = 12045
it all checks out, assuming 365 days in a year.
i assumed 33 years.
i'm not sure what you means by 33/4.
you could have meant 33 or 34 years.
you could have meant 33/4 = 8.25 years.
use the same formula and make any assumption you want and you'll get the answer you're looking for.
just keep in mind.....
r = annual interest rate % divided by number of compounding periods per year divided by 100.
n = number of years times number of compounding periods per year.
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website! Find the principal needed now to get the given amount; that is, find the present value.
To get $3000 after 33/4 years at 5% compounded daily.
The present value of $ 3000 is?$______
(Round to the nearest cent as needed.)
PV of a FV amount of $3,000, for 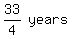 at 5% interest, compounded daily (360/365 days):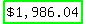 
|
|
|
