Question 1088524: find what fraction of the altitude of a tetrahedron must be cut off by a plane parallel to the base of the tetrahedron such that the volume of the cut off tetrahedron is one third of the original volume.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Compared to the original tetrahedron, the smaller tetrahedron cut off is a similar shape, meaning a scaled-down version.
For similar shapes, the ratios of lengths (L and l), surface areas (A and a), and volumes (V and v) are related by
 and and  . .
In this case, if  is the fraction of the altitude of a tetrahedron cut off by a plane parallel to the base of the tetrahedron, is the fraction of the altitude of a tetrahedron cut off by a plane parallel to the base of the tetrahedron,
and the volume of the small cut off tetrahedron is one third of the original volume,
 --> -->  . .
The exact result is an irrational number, so it cannot be expressed as a fraction.
However, the fractions 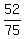 and and  are good approximate values. are good approximate values.
|
|
|