Question 1088451: If a,b,c i.e the coefficients of the quadratic equation ax^2+bx+c=0 are in A.P and the one root of this given equation is 2, then find the other root?
a)3/4
b)-3/4
c)-5/4
d)-5/2
My attempt.
Since this is a competitive exam question,I first tried to solve mentally. i.e by putting a=1 which suggested me that b=1+d and c=1+2d where d=common difference
Now I made an equation,
x^2+(root+2)+2*root=0
compare with above made equation
x^2+bx+c=0 since a=1 i putted
then b=root+2 and c=2*root, and then it became like unsolvable for me!!! Please help,thanks!!!
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If a,b,c i.e the coefficients of the quadratic equation ax^2+bx+c=0 are in A.P and the one root of this given equation is 2, then find the other root?
a)3/4
b)-3/4
c)-5/4
d)-5/2
My attempt.
Since this is a competitive exam question,I first tried to solve mentally. i.e by putting a=1 which suggested me that b=1+d and c=1+2d where d=common difference
Now I made an equation,
x^2+(root+2)+2*root=0
compare with above made equation
x^2+bx+c=0 since a=1 i putted
then b=root+2 and c=2*root, and then it became like unsolvable for me!!! Please help,thanks!!!
~~~~~~~~~~~~~~~~~~~~~~~~
You are given that
 = 0. (1)
Since a, b and c are AP, b = = 0. (1)
Since a, b and c are AP, b = 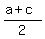 . (2)
It is a characteristic property of any AP.
See the lesson One characteristic property of arithmetic progressions in this site.
In (1), replace b by . (2)
It is a characteristic property of any AP.
See the lesson One characteristic property of arithmetic progressions in this site.
In (1), replace b by 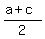 and divide both sides of (1) by "a". You will get an equivalent equation and divide both sides of (1) by "a". You will get an equivalent equation
 = 0. (3)
Since x= 2 is the root of this equation (Given !), you can substitute x= 2 into (3). You will get = 0. (3)
Since x= 2 is the root of this equation (Given !), you can substitute x= 2 into (3). You will get
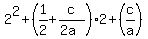 = 0, or = 0, or
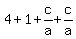 = 0, or = 0, or
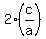 = -5 and finally = -5 and finally  = =  .
Now your equation (3) takes the form .
Now your equation (3) takes the form
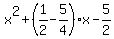 = 0, or, which is the same, = 0, or, which is the same,
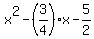 = 0. (4)
You may check that x= 2 is the root of this equation.
By the way, you actually found THE COEFFICIENTS of your original equation (1)
under the assumption that the leading coefficient "a" is equal to 1.
These coefficients are 1, = 0. (4)
You may check that x= 2 is the root of this equation.
By the way, you actually found THE COEFFICIENTS of your original equation (1)
under the assumption that the leading coefficient "a" is equal to 1.
These coefficients are 1,  and and  , and you can check that they form an AP.
Now you can solve your equation (4) and to find the other root.
I will leave it to you. , and you can check that they form an AP.
Now you can solve your equation (4) and to find the other root.
I will leave it to you.
Solved.
H a p p y l e a r n i n g ! !
I am glad that I am still able to solve competitive problems !!
-----------------
There is a bunch of lessons on arithmetic progressions in this site:
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Mathematical induction and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Arithmetic progressions".
You have, actually, three free of charge online textbooks in Math in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK
- ALGEBRA-II - YOUR ONLINE TEXTBOOK
- GEOMETRY - YOUR ONLINE TEXTBOOK
The level of these textbooks is exactly "SHCOOL +" adequate to the level of students who really want to know the school math
and wish participate in school Math competitions.
As I did in my youth school years . . .
|
|
|