SOLUTION: A and B walk around a circular track . A and B walk at a speed of 2 rounds per hour and 3 rounds per hours respectively . If they start at 8 AM from the same point in opposite dire

1.  Let answer first more simple question:


        if they start from the same point in opposite directions at 8 am, when they meet each other next time ?


    It is clear that they will meet each other next time when the sum of distances covered by each along the circumference 
    becomes EXACTLY equal to one circle  length.

    Next, the rate of A is 2 rounds per hour; the rate of B is 3 rounds per hour;

    HENCE, their relative speed is (2+3) = 5 rounds per hour.


    So, they meet each other next time in 12 minutes = ,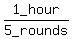 
        at 8:12 am.


2.  From his point, it is clear that they will meet each other EVERY 12 minutes.


    Now, how much room there is in 90 minutes for 12 minute intervals ?


    It is easy question:  = 7.5 times.


3.  So, if you start count from 8:00 when A and B are close to each other for the first time, you will count 7 times more when they meet each other.