.
If y = 3cosA + 4sinA, then (divide both sides by 5. You will get)
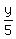 =
= 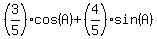 .
Since
.
Since 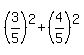 = 1, there exist the angle
= 1, there exist the angle  such as
such as
 =
=  ,
,  =
=  .
Then we have
.
Then we have
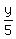 =
= 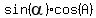 +
+ 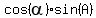 =
= 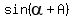 .
Since -1 <= sin(alpha +A) <= 1, then -1 <
.
Since -1 <= sin(alpha +A) <= 1, then -1 < 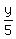 <= 1, or
- 5 <= y <= 5.
From this point, you can easily convince yourself and prove that The equation y = 3cosA + 4sinA has a real solution
if and only if y belongs to the segment [-5,5].
Answer. The equation y = 3cosA + 4sinA has a real solution if y is in the segment [-5,5].
<= 1, or
- 5 <= y <= 5.
From this point, you can easily convince yourself and prove that The equation y = 3cosA + 4sinA has a real solution
if and only if y belongs to the segment [-5,5].
Answer. The equation y = 3cosA + 4sinA has a real solution if y is in the segment [-5,5].