SOLUTION: If cosA-sinA=√2sin A then cosA+sinA equals

Algebra ->  Trigonometry-basics -> SOLUTION: If cosA-sinA=√2sin A then cosA+sinA equals      Log On


   

Question 1088217: If cosA-sinA=√2sin A then cosA+sinA equals
Answer by ikleyn(52903) About Me  (Show Source):
You can put this solution on YOUR website!
.
If cos(A) - sin(A) = sqrt(2)*sin(A) then cos(A) + sin(A) equals
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

You are given

cos(A) - sin(A) = sqrt(2)*sin(A).    (1)


Divide both sides by sqrt%282%29. You will get

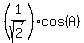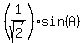%281%2Fsqrt%282%29%29%2Acos%28A%29 - %281%2Fsqrt%282%29%29%2Asin%28A%29 = sin(A).


It is the same as

%28sqrt%282%29%2F2%29%2Acos%28A%29 - %28sqrt%282%29%2F2%29%2Asin%28A%29 = sin(A).      (2)


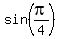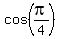Now recall that sqrt%282%29%2F2 = sin%28pi%2F4%29 = cos%28pi%2F4%29.


Therefore, you can re-write (2) in the form

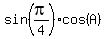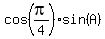sin%28pi%2F4%29%2Acos%28A%29 - cos%28pi%2F4%29%2Asin%28A%29 = sin(A).


Using the adding/subtracting formula for sine, it is the same as

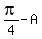sin%28pi%2F4+-+A%29 = sin%28A%29,                         (3)


which implies EITHER

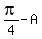    pi%2F4+-+A = A + 2k%2Api,                     (4)    

OR

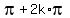    pi%2F4+-+A + A = pi+%2B+2k%2Api                   (5)

where k is any integer.


Equation (5) has no solution, obviously.

Equation (4) has the solution

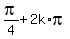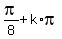    2A = pi%2F4%2B+2k%2Api,   or   A = pi%2F8+%2B+k%2Api.      (6)


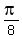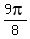Actually, we have two cases:  A = pi%2F8  and  A = 9pi%2F8.


It is well known fact that 

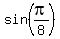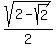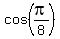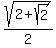sin%28pi%2F8%29 = sqrt%282-sqrt%282%29%29%2F2,  cos%28pi%2F8%29 = sqrt%282%2Bsqrt%282%29%29%2F2.

    (see the lesson Miscellaneous Trigonometry problems in this site).


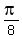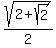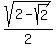So, if A = pi%2F8,   then  cos(A) + sin(A) = sqrt%282%2Bsqrt%282%29%29%2F2 + sqrt%282-sqrt%282%29%29%2F2.


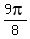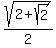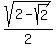    If A = 9pi%2F8,  then  cos(A) + sin(A) = -( sqrt%282%2Bsqrt%282%29%29%2F2 + sqrt%282-sqrt%282%29%29%2F2 ).

Answer.  If  cos(A) - sin(A) = sqrt(2)*sin(A)   then

                    a)  A = 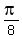pi%2F8  or  A = 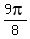9pi%2F8,   and

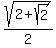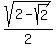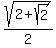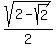                    b)  cos(A) + sin(A)  equals   sqrt%282%2Bsqrt%282%29%29%2F2 + sqrt%282-sqrt%282%29%29%2F2   or   -(sqrt%282%2Bsqrt%282%29%29%2F2 + sqrt%282-sqrt%282%29%29%2F2).

Solved.