SOLUTION: If {{{ a + b = a/b + b/a }}} where a and b are positive integers, find the value of {{{ a^2 + b^2 }}}. Thank you.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: If {{{ a + b = a/b + b/a }}} where a and b are positive integers, find the value of {{{ a^2 + b^2 }}}. Thank you.      Log On


   

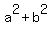Question 1087653: If +a+%2B+b+=+a%2Fb+%2B+b%2Fa+ where a and b are positive integers, find the value of +a%5E2+%2B+b%5E2+.
Thank you.
Found 2 solutions by math_helper, Edwin McCravy:
Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!
+highlight%28+a%5E2+%2B+b%5E2++=+ab%28a%2Bb%29+%29 ; a,b both positive integers
—
To see the answer is equivalent to the original, (since a>0 & b>0) divide both sides by ab to get back to the original:
++%28a%5E2+%2B+b%5E2%29%2F%28ab%29+=+ab%28a%2Bb%29%2F%28ab%29+
+++a%2Fb+%2B+b%2Fa++=++a%2Bb+
—
Edit 7/15/17: Edwin is right, I just thought you wanted an alternate form of a%5E2%2Bb%5E2 in terms of a & b.

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
The tutor above thought you just wanted an alternate expression for a2+b2.
But you wanted a numerical solution.

If +a+%2B+b+=+a%2Fb+%2B+b%2Fa+ where a and b are positive integers,
find the value of 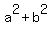+a%5E2+%2B+b%5E2+.
By inspection we see that a=1 and b=1, and a%5E2%2Bb%5E2=1%5E2%2B1%5E2=1%2B1=2.
is a solution.  But is that the ONLY possible solution?

We might guess that that is the only solution, but guessing
doesn't count!  :)

So let's see if we can prove that it is the only solution.

+a+%2B+b+=+a%2Fb+%2B+b%2Fa+

Clear of fractions and set up the quadratic in b

+a%5E2b+%2B+ab%5E2+=+a%5E2+%2B+b%5E2+

ab%5E2-b%5E2%2Ba%5E2b-a%5E2=0

%28a-1%29b%5E2%2B%28a%5E2%29b-a%5E2=0

The discriminant must be a perfect square for b to
even be rational:



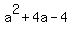So a%5E2%2B4a-4 must be a perfect square, say p2

a%5E2%2B4a-4=p%5E2

a%5E2%2B4a-4-p%5E2=0

The discriminant must also be a perfect square for 'a' to
even be rational:

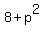discriminant=4%5E2-4%281%29%28-4-p%5E2%29=16%2B16%2B4p%5E2=32%2B4p%5E2=4%288%2Bp%5E2%29

So 8%2Bp%5E2 must be a perfect square, say q2

8%2Bp%5E2=q%5E2

q%5E2-p%5E2=8

%28q-p%29%28q%2Bp%29=8

The only possibilities are

q-p=1, q+p=8, but that gives a fraction solution.
q-p=2, q+p=4 which gives the only solution in integers,
q=3, p=1 

So

a%5E2%2B4a-4-p%5E2=0

becomes

a%5E2%2B4a-4-1%5E2=0

a%5E2%2B4a-5=0

%28a%2B5%29%28a-1%29=0

So we have proved that 'a' can only be 1.

+a+%2B+b+=+a%2Fb+%2B+b%2Fa+

+1+%2B+b+=+1%2Fb+%2B+b%2F1+

b%2Bb%5E2=1%2Bb

b%5E2=1

And now b can only be 1 also.

Therefore the only solution for a and b in positive integers is 
a = b = 1, and 

a2+b2 = 12+12 = 1+1 = 2.

Edwin