SOLUTION: Find the equation of parabola whose focus is (-8, -2) and equation of directrix is y = 2x - 9

We use the definition of a parabola:

A parabola is the set of points that are equidistant
from the focus (a point) and the directrix (a line).

Let (x,y) be an arbitrary point on the parabola. 

Essentially we set the lengths of the two green lines 
equal to each other. 

The distance from the arbitrary point (x,y) to the 
focus is gotten by the formula for the distance
between two given points:

 

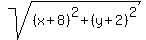The distance from the arbitrary point (x,y) to the
directrix is gotten by the formula for the distance 
from a given point to a given line.

We write the equation of the directrix y = 2x - 9,
as 2x-y-9 = 0, then the distance from the focus to 
the directrix is:



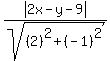
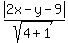
So we set those two distances equal to each other:



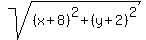
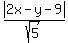Square both sides:









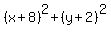
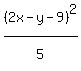
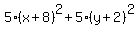
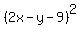
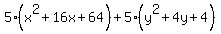
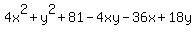
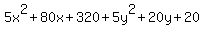
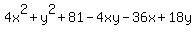That simplifies to



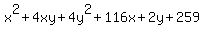
Edwin