Question 1087562: Larry's evening is spent reading and watching TV. He can spend no more than 4 hours total on these activities, and he wants to spend more time reading than watching TV. Which graph represents this situation?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! The question is incomplete. The answer choices are missing. Also, the problem doesn't state what x should be or what y should be. However it seems like it should be this
x = amount of time spent reading
y = amount of time watching tv
which of course is an assumption that may be wrong. Let me know if it is or not. Thank you.
-----------------------------
If that assumption is correct, then we know that  according to the constraint that "He can spend no more than 4 hours total on these activities". We can solve for y to get according to the constraint that "He can spend no more than 4 hours total on these activities". We can solve for y to get 
Keeping with the same assumption about x and y, we're told that "he wants to spend more time reading than watching TV" so this means 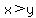 which turns into which turns into 
Because we don't want negative time values for any activity, we must make sure that x or y can't be negative. That means we add in the further constraints that  and and  . Essentially the solution set can only be found in the first quadrant (which is the upper right hand quadrant) . Essentially the solution set can only be found in the first quadrant (which is the upper right hand quadrant)
-----------------------------
If we plot  and and  together, we get the following together, we get the following

(Image generated by GeoGebra which is free graphing software)
The graph of  is shown in red (note the solid boundary line) and is shown in red (note the solid boundary line) and  is shown in blue (the boundary line is dashed). The overlap of the blue and red regions forms the purple region which will help us get to the solution set, or feasible region. is shown in blue (the boundary line is dashed). The overlap of the blue and red regions forms the purple region which will help us get to the solution set, or feasible region.
Here is just the overlapped purple region with the unnecessary regions erased

And here is the final solution set. I erased the portion below the x axis. This is because y can't be negative (we set the constraint  ) )

One such point in this set is (x,y) = (2,1). We can see that x > y is true (he spends 2 hours reading which is more than 1 hour of watching tv). Also we see that x+y <= 4 is true as well (he spends 2+1 = 3 hours which is less than the 4 hour constraint).
Any points on the solid boundary line (that are adjacent to the purple shaded region) are solutions. For example, (x,y) = (3,1) is a solution.
In contrast, points on the dashed boundary line are not solutions. Something like (x,y) = (1,1) isn't in the solution set because x > y isn't true for these values.
-----------------------------
Keep in mind that this is all based on the assumptions I made about x and y. Without knowing the full problem and seeing those answer choices, I'm not 100% sure I assigned the right values.
|
|
|