Question 1087406: How would you do these?:
1. x^2 + 7x + 10
2. x^2 – 4 + 3
3. x^2 + x – 20
4. 3x^2 – 17x + 10
5. 5x^2 – 6x + 1
6. 4x^2 + 28x + 49
Answer by ValorousDawn(53)   (Show Source): (Show Source):
You can put this solution on YOUR website! I will assume you are instructing to solve the above by way of factoring, then utilizing the zero product property. I will first show the legitimacy of the following, then demonstrate such on your problems. If you do not care to see why factoring gives you your answer, you may scroll down further.
We start with an already factored quadratic. For different values h and k, we have  . .
Invoke the zero product property. Anything multiplied by zero results in zero itself. Therefore, if 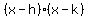 equals 0, one the has to equal zero; otherwise, it cannot equal zero. equals 0, one the has to equal zero; otherwise, it cannot equal zero.
We can use either situation. If  , then , then  . .
Then, if you add h to both sides,  . .
The same logic applies to if  . .  , then , then  . .
All together, we have if  , x wil have to equal either x or k. , x wil have to equal either x or k.
More simply, we can write this as  . .
OK, so if an equation is factored, we can solve it. However, if it is not, we cannot (yet!) solve it. The goal now is to discern a way to make our expressions factored.
Look once more at 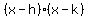 and expand it. Through FOIL, you arrive at and expand it. Through FOIL, you arrive at  . .
Specifically at 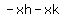 , this can be made simplified. Note that both of them have a , this can be made simplified. Note that both of them have a  component. You can factor this out of each of them. You will then have -x times h + -x times k. Then you can factor the entire expression to get component. You can factor this out of each of them. You will then have -x times h + -x times k. Then you can factor the entire expression to get 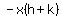 . .
Thus, 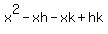 becomes becomes 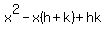 . What does this tell us? Looking at the general form of a quadratic expression . What does this tell us? Looking at the general form of a quadratic expression  , they look alike. It tells us that if we want a nice factored form of , they look alike. It tells us that if we want a nice factored form of 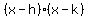 , we will just have to find values of a,b and c that work with the conditions given to us. This will be your methodology for attacking factoring problems. Find two numbers h and k such that: , we will just have to find values of a,b and c that work with the conditions given to us. This will be your methodology for attacking factoring problems. Find two numbers h and k such that:
They multiply to give you the third number, and add to give you the second number.
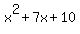 This will be 5 and 2, since 5*2=10, and 5+2=7. This will be 5 and 2, since 5*2=10, and 5+2=7. 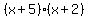 
 Note that we can use negatives! Our options are (1,3) and (-1,-3). The first does not work since 1+3 is not -4. However, the second does work, since -1 -3 is -4. Note that we can use negatives! Our options are (1,3) and (-1,-3). The first does not work since 1+3 is not -4. However, the second does work, since -1 -3 is -4. 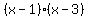 
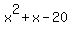 Our options are (-1,20), (1, 20), (-2, 10), (2, -10), (-4, 5), (4, -5). Checking these, only (-4, 5) works, since -4+5=1, and -4*5=-20. Our options are (-1,20), (1, 20), (-2, 10), (2, -10), (-4, 5), (4, -5). Checking these, only (-4, 5) works, since -4+5=1, and -4*5=-20. 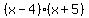 
The latter ones are more complex. Our simple tools no longer work. This is because they do not factor into 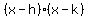 , but something of the form , but something of the form 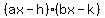 . These multiply out to . These multiply out to  . .
Looking at the terms 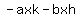 , note that each of them has the -x in common. Factoring this out gives -x times ak + -x times bh. This can then be factored to , note that each of them has the -x in common. Factoring this out gives -x times ak + -x times bh. This can then be factored to 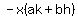 . .
Our expression is then 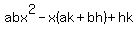 . .
This is a handful. We want four numbers a,b,h and k such that a*b is the first number, ak+bh is the second and hk the latter. This is accomplished more succinctly with what is known as the box method, or via guessing and checking. The actual process is difficult to detail, but I will leave the answers to the remaining. (I recommend you Google the former since I am not able to do it justice!)
 . . 
 . . 
 . . 
|
|
|