.
1. Find the intersection point of these lines.
For it, solve the system of equations to get (x,y) = (1,5) as the intersection point.
(I solved it mentally - hence, you can do the same . . . )
2. Find the distance from the intersection point to the origin.
It is  =
=  .
Thus the radius of the circle is
.
Thus the radius of the circle is  units.
3. Then the area of the circle is
units.
3. Then the area of the circle is  =
= 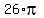 .
.
Solved.