.
You have actually two options.
1. The "rational root theorem" says that if you are given a polynomial with integer coefficients and the leading coefficient 1
at the highest degree of x (as in your case), then the integer roots of the polynomial (IF IT HAS INTEGER ZEROES)
are among integer divisors of its constant term.
So, in your case you need to check integer divisors of your constant term 9.
They are 1, -1, 3, -3, 9 and -9.
2. Another option is to make the plot of a polynomial, which can tell you a lot about its roots.
See below:
Plot y = 
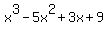In THIS case, the plot says that x = -1 is the root of multiplicity 1 and x = 3 is the root of multiplicity 2.
Surely, the plot gives the visual hint only.
After getting this hint you MUST check manually that the specific numbers are the roots/the root.
3. If you assure that x= a is the root, then the linear binomial (x-a) is a factor of your polynomial.
In your case the numbers -1 and 3 are zeroes, so the binomials (x+1) and (x-3) are the factors, and the factoring is
f(x) = (x+1)*(x-3)^2.
Solved.
