SOLUTION: a,b,c are roots of 2x^3+x^2-7, find value of (a/b+b/a)+(b/c+c/b)+(c/a+a/c)

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: a,b,c are roots of 2x^3+x^2-7, find value of (a/b+b/a)+(b/c+c/b)+(c/a+a/c)      Log On


   

Question 1087154: a,b,c are roots of 2x^3+x^2-7, find value of (a/b+b/a)+(b/c+c/b)+(c/a+a/c)
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
a,b,c are roots of 2x^3+x^2-7, find value of (a/b+b/a)+(b/c+c/b)+(c/a+a/c)
~~~~~~~~~~~~~~~~~~~~ 

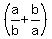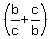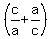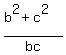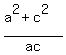  %28a%2Fb%2Bb%2Fa%29 + %28b%2Fc%2Bc%2Fb%29 + %28c%2Fa%2Ba%2Fc%29 = %28a%5E2+%2B+b%5E2%29%2Fab + %28b%5E2+%2B+c%5E2%29%2Fbc + %28a%5E2%2Bc%5E2%29%2Fac =  = 

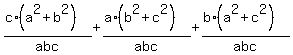= %28%28a%5E2c+%2B+b%5E2c%29+%2B+%28ab%5E2+%2B+ac%5E2%29+%2B+%28a%5E2b+%2B+bc%5E2%29%29%2Fabc = (regroup)

=  = 

=  = 

   - 3 = 

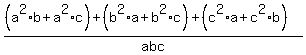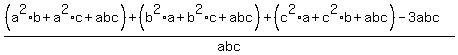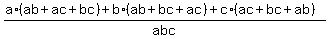= %28%28a+%2B+b+%2B+c%29%2A%28ab+%2B+ac+%2B+bc%29%29%2Fabc - 3.    (1)


Now, according to the Vieta's theorem for the cubic polynomial,

a + b + c = -1%2F2,         (2)  

ab+ ac + bc = 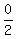0%2F2 = 0,    (3)

abc = 7%2F2.                (4)


Substitute (2), (3) and (4) into (1) and calculate the answer:


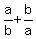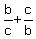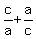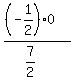a%2Fb%2Bb%2Fa + b%2Fc%2Bc%2Fb + c%2Fa%2Ba%2Fc = +%28%28-1%2F2%29%2A0%29%2F%287%2F2%29 - 3 = -3.

Solved.


The lesson to learn from this solution is highlight%28THIS%29:

    You do not need to solve the original equation to get the answer.

    You can get the answer manipulating THE COEFFICIENTS of the original equation.



To see more samples of similar solved problems, see the lessons
    - HOW TO evaluate functions of roots of a square equation
    - HOW TO evaluate functions of roots of a cubic and quartic equation
in this site.


Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Evaluation, substitution".