SOLUTION: If a positive integral divisor of 16200 is selected of random,given that it is even,the chance that it will have exactly four divisors is

Algebra ->  Probability-and-statistics -> SOLUTION: If a positive integral divisor of 16200 is selected of random,given that it is even,the chance that it will have exactly four divisors is       Log On


   

Question 1087145: If a positive integral divisor of 16200 is selected of random,given that it is even,the chance that it will have exactly four divisors is
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
16200=81%2A2%2A100=2%5E3%2A3%5E4%2A5%5E2 has many positive integral divisors,
from 1=1%2A1%2A1=2%5E0%2A3%5E0%2A5%5E0 to 16200=81%2A2%2A100=2%5E3%2A3%5E4%2A5%5E2 .
All of those divisors of the form
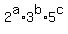2%5Ea%2A3%5Eb%2A5%5Ec ,
where %22a+%2C+b+%2C+and%22c
are integers such that
system%280%3C=a%3C=3%2C0%3C=b%3C=4%2C0%3C=c%3C=2%29 .
The ones that are odd must have a%2B1=1 <--> a=0 .
There are 1%2A%284%2B1%29%2A%282%2B1%29=1%2A5%2A3=15 of them.
The other 60-15=45 are even, and have 1%3C=a%3C=3 .

Each of those 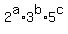2%5Ea%2A3%5Eb%2A5%5Ec divisors will have
we need one of those factors to be 1 .
The other two factors could be 4 and 1 , or 2 and 2 .
There is no other way.

For one of the factors to equal 4 , and the other two to equal 1 ,
it must be a%2B1=4 <--> a=3 ,
because a%2B1=1 <--> a=0 is not possible with an even divisor,
so the only way to do that is
system%28a=3%2Cb%2B1=1%2Cc%2B1=1%29 <--> system%28a=3%2Cb=0%2Cc=0%29 <--> 2%5Ea%2A3%5Eb%2A5%5Ec=2%5E3%2A3%5E0%2A5%5E0=8%2A1%2A1=8 i.
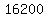That gives us 1 even divisors of 16200 with exactly four divisors.

All three factors can be equal to 2 :
a%2B1=2 <--> a=1 ,
b%2B1=2 <--> b=1 , and
c%2B1=2 <--> c=1 .
Choosing one of the factors than can equal 1 to be 1 , as in
b%2B1=1 <--> b=0 , or
c%2B1=1 <--> c=0 ,
and the other two factors to be 2 ,
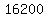we get 2 more even divisors of 16200 with exactly four divisors
2%5Ea%2A3%5Eb%2A5%5Ec=2%5E1%2A3%5E0%2A5%5E1=2%2A1%2A5=10 , and
2%5Ea%2A3%5Eb%2A5%5Ec=2%5E1%2A3%5E1%2A5%5E0=2%2A3%2A1=6 .

In sum, we can find 1%2B2=3 ways, and only 3 ways
to make an even divisor of 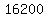16200 with exactly four divisors.
The divisors of 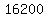16200 with exactly four divisors are
8, 10, and 6,
and they are only 3 of the 45
positive integral divisors of 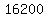16200 that are even.
If a positive integral divisor of 16200 is selected of random,
and is one of the 45 that are even,
the chance that it will have exactly four divisors is
3%2F45=highlight%281%2F15%29