Question 1087064: find the probability of getting vowels in the first, third, and sixth place when all the letters of the word ORANGE are arranged in all possible ways.
Found 2 solutions by math_helper, mathmate:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Pr(vowel in 1st, 3rd, and 6th place) =
(#ways that O,A,E can be arranged in 1st, 3rd, and 6th place) / (#ways of arranging letters O,R,A,N,G,E)
—
#ways of arranging letters O,R,A,N,G,E = 6!
#ways that O,A,E can appear in 1st, 3rd, and 6th place = 3! * 3! (for each vowel arrangement, you can have the remaining 3 consonants arranged in 3! ways)
—
Pr(vowel in 1st, 3rd, and 6th place) = (3!*3!)/6! = 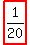
—
Edit 7/8/17 : Fixed answer to account for consonant arrangement which was missing from my first answer. Thanks mathmate.
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website! Question:
Find the probability of getting vowels in the first, third, and sixth place when all the letters of the word ORANGE are arranged in all possible ways.
Solution:
Examine problem: word ORANGE has 3 distinct vowels (OAE) and 3 distinct consonants (RNG).
To find the number of arrangements with three vowels in specific places, we first place the vowels, one by one, in 3*2*1=6 ways. Similarly there are 6 ways to place the consonants.
=========================================================
* The 6 ways are obtained as follows:
for the first position, we have three choices of letters
for the second position, we have only two letters left, since one was used
earlier for the first position.
similarly, for the sixth position, we have already used up 2 of three
letters, so there is only one choice left.
Therefore, the total number of choices to fill the vowels is 3*2*1=6, or
number of arrangements = 3!
The same principle can be applied to filling the consonants.
=========================================================
There is a total of 6*6=36 ways to place vowels and consonants in designated locations.
The total number of "words" formed using the six distinct letters is 6*5*4*3*2*1=720
Thus the probability of getting vowels in specific places from a random word is 36/720=1/20
|
|
|