Question 1086901: What kind of sequence is this?
191, 175, 159, 143
arithmetic, geometric, both, neither
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
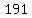 , ,  , , 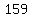 , , 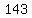 ,... ,...
see if there is constant difference between terms


so, 
check:
 , ,
 , ,
 , ,
 ,... ,...
find 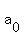 => =>



so, in general n-th term formula is:
 where where  = = , , , , ,.... ,....
since by definition, an arithmetic sequence goes from one term to the next by always adding (or subtracting) the same value known as "common difference", in your case we have an 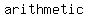 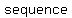
|
|
|