|
Question 1086693: find equation of the circle passing through A(1,4) , B(-1,8) and tangent to the line x + 3y - 3 = 0
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
Answer by ikleyn(52887)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
find equation of the circle passing through A(1,4) , B(-1,8) and tangent to the line x + 3y - 3 = 0
~~~~~~~~~~~~~~~~~~~~
The center of the circle lies on the perpendicular bisector to the segment with endpoints A and B.
The midpoint is C = (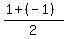 , ,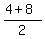 ) = (0,6).
The segment AB has the slope ) = (0,6).
The segment AB has the slope 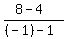 = = 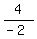 = -2; hence, the perpendicular line has the slope = -2; hence, the perpendicular line has the slope  = 0.5.
The equation of the straight line with the slope 0.5 passing through (0,6) is
y-6 = 0.5*(x-0), or y = 0.5x + 6. (1)
Now we need to find the center as the point (x,y) which lies at the straight line (1) and is equidistant from the point A and
from the given straight line.
The distance from the point (x,y) to A is = 0.5.
The equation of the straight line with the slope 0.5 passing through (0,6) is
y-6 = 0.5*(x-0), or y = 0.5x + 6. (1)
Now we need to find the center as the point (x,y) which lies at the straight line (1) and is equidistant from the point A and
from the given straight line.
The distance from the point (x,y) to A is 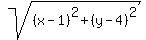 .
The distance the point (x,y) to the line x + 3y -3 = 0 is .
The distance the point (x,y) to the line x + 3y -3 = 0 is
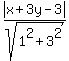 = =  (see the lesson The distance from a point to a straight line in a coordinate plane in this site).
So, your equation is (see the lesson The distance from a point to a straight line in a coordinate plane in this site).
So, your equation is
 = = 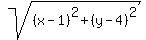 ,
or, when squared, ,
or, when squared,
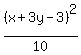 = = 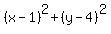 . (2)
The second equation is
y = 0.5x + 6. (3)
When you substitute (3) into (2), you will get a single equation for x: . (2)
The second equation is
y = 0.5x + 6. (3)
When you substitute (3) into (2), you will get a single equation for x:
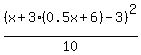 = = 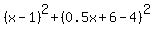 .
Simplify it step by step: .
Simplify it step by step:
 = =  ====> ====> 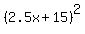 = = 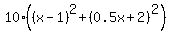 ====> ====> 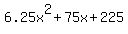 = = 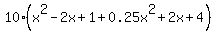 ====> ====>
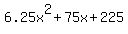 = = 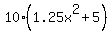 ====> ====> 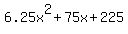 = = 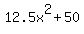 ====> ====> 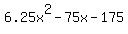 = 0 ====> = 0 ====>  = 0 ====> = 0 ====>
 = =  .
There are two solutions: .
There are two solutions:  = 14 and = 14 and  = -2.
The corresponding centers are (x,y) = (14,13) and (x,y) = (-2,5).
The distance from (14,13) to (1,4) is = -2.
The corresponding centers are (x,y) = (14,13) and (x,y) = (-2,5).
The distance from (14,13) to (1,4) is 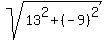 = =  = =  .
The distance from (-2,5) to (1,4) is .
The distance from (-2,5) to (1,4) is 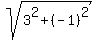 = =  .
So, there are two circles, and their equations are .
So, there are two circles, and their equations are
 = 250 and = 250 and 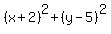 = 10. = 10.
Solved.
For many other similar solved problems see the lesson
- Find the standard equation of a circle
in this site.
|
|
|
| |