Question 1086637: The letters of the word STATISTICS are arranged randomly.
What is the probability the arrangement will start and end with an S?
Found 4 solutions by jim_thompson5910, Edwin McCravy, KMST, ikleyn:
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! There are 10 letters in the word STATISTICS.
So there are 10 slots needed to be filled. The first and last slot (slot1, slot10) are reserved for the letter S. There is only one way to do this. This is because the three S letters are not unique from one another.
The remaining middle 8 slots (slot2 through slot9) are open to be filled with 8 choices drawn from this list: {T,A,T,I,S,T,I,C}
There are 8! = 8*7*6*5*4*3*2*1 = 40,320 different ways to fill those 8 slots if we can tell the repeating letters apart.
Since we can't tell them apart, we have to divide by 3!*2! to deal with the fact that the letter "T" repeats three times and the letter "I" repeats twice.
We now have (40320)/(3!*2!)=(40320)/(6*2)=(40320)/(12)=3360
Meaning that there are 3,360 ways to arrange the letters so that the arrangement will start and end with an S
We will use the value 3360 later, so let's make A = 3360
------------------------------------------------------------------------------------
If we ignore the restrictions, and simply count the number of arrangements, then we have (10!)/(3!*3!*2!) = 50400 different arrangements.
We'll call this value B = 50400
------------------------------------------------------------------------------------
Divide the values of A and B to get A/B = 3360/50400 = 1/15
The answer as a fraction is 1/15
The answer in decimal form is approximately 0.0667 (use a calculator to compute 1/15 = 0.0667)
The answer in percentage form is approximately 6.67% (move the decimal point over 2 spots to the right)
Edit: My initial answer was incorrect, but I have fixed it
Answer by Edwin McCravy(20060)  (Show Source):
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! There are 10 characters, and 3 of them are S,
so when picking your first character,
the probability of picking an S would be
 .
After that, there would be 9 characters left, including two S characters.
Then the probability id picking an S for last character,
after having picked an S for fist character would be  .
So, the probability that a rearrangements of the letters in STATISTICS
would start and end with S is
 .
ANOTHER WAY:
There are  possible arrangements.
If you labeled the letters so as to distinguish one S from another S, one T from another T, and one I from the other I, you would see that many different arrangements.
If we are to make arrangements starting and ending with S,
there are 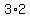 ways to choose which S will be at either end,
and there are 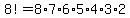 ways to arrange the 8 middle characters.
That makes for 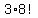 different arrangements starting and ending wit S,
out of the  possible arrangements.
That is 
Answer by ikleyn(52858)  (Show Source):
You can put this solution on YOUR website! .
The term "arrangement" may have two DIFFERENT meaning in this problem.
One meaning is "permutation" and the other meaning is "word", where we do not distinct indistinguishable letters.
So, strictly speaking, the formulation is ambiguous.
|
|
|
