.
Notice that if x is negative, then  is negative and, therefore, can not be greater or equal to 5.
Hence, the solution set {x} is among positive real numbers.
Assuming that x is positive, multiply both sides of
is negative and, therefore, can not be greater or equal to 5.
Hence, the solution set {x} is among positive real numbers.
Assuming that x is positive, multiply both sides of  >=5 by x.
Since x is positive, you can keep the same inequality sign.
So, your inequality becomes 6 >= 5x.
Now divide both sides by the positive number 5. You will get an equivalent inequality x <=
>=5 by x.
Since x is positive, you can keep the same inequality sign.
So, your inequality becomes 6 >= 5x.
Now divide both sides by the positive number 5. You will get an equivalent inequality x <= 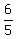 .
.
Answer. The solution set is 0 < x <= 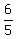 .
.
Illustration:
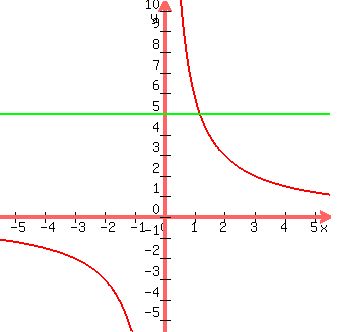
Plots y =  (red) and y = 5 (green)
(red) and y = 5 (green)