SOLUTION: When polynomial P(x) is divided by x + 1, x + 2, and x + 3, the remainders are 2, 3, and 6, respectively. Find the remainder when P(x) is divided by (x + 1)(x + 2)(x + 3).

Let  to see if that is a possibility.

Then, using the remainder theorem: 













Solve this system by elimination or other method:



Solution:  A=7, B=13, C=9

So

When  is multiplied out, 
we get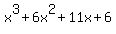 

Dividing by long division:
                        1 
x³+6x²+11x+6)x³+7x²+13x+9
             x³+6x²+11x+6
                 x²+ 2x+3  

Answer: x²+2x+3

Edwin

We are given that 

     "when polynomial P(x) is divided by x + 1, x + 2, and x + 3, the remainders are 2, 3, and 6, respectively."


According to the Remainder theorem, it is equivalent to these equalities:

    P(-1) = 2,    (1)
    P(-2) = 3,    (2)
    P(-3) = 6.    (3)


Now, the question is to find a remainder polynomial R(x) after dividing P(x) by (x+1)*(x+2)*(x+3):

    P(x) = g(x)*(x+1)*(x+2)*(x+3) + R(x).     (4)


It is clear that the polynomial R(x) has the degree <= 2, so we can write

   R(x) = Ax^2 + Bx + C.                      (5)


Substituting x= -1, x= -2 and x= -3 into (4), from (1), (2) and (3) we have 

    P(-1) = g(-1)*0 + R(-1) = 2,   i.e.   R(-1) = 2;     (6)
    P(-2) = g(-2)*0 + R(-2) = 3,   i.e.   R(-2) = 3;     (7)
    P(-3) = g(-3)*0 + R(-3) = 6,   i.e.   R(-3) = 6.     (8)


So, we need to find coefficients A, B and C of the remainder polynomial R(x) from conditions (6), (7) and (8).


Equation (6) gives

    A*(-1)^2 + B*(-1) + C = 2,   or   A - B + c = 2;     (9)
   
Equation (7) gives

    A*(-2)^2 + B*(-2) + C = 3,   or   4A - 2B + c = 3;   (10)

Equation (8) gives

    A*(-3)^2 + B*(-3) + C = 6,   or   9A - 3B + c = 6.   (11)


Thus you have this system of 3 equations to find A, B and C:

 A -  B + c = 2,
4A - 2B + c = 3,
9A - 3B + c = 6.


Solve it by any method you want/you know (Substitution, Elimination, Determinanf (= Cramer's rule) ). You will get  A = 1,  B= 2  and  C = 3.


So, the remainder, which is under the question, is R(x) = x^2 + 2x + 3.