.
The remainder  of x^3+ax+b when divided by (x^2-1) is x+2. Find a and b.
of x^3+ax+b when divided by (x^2-1) is x+2. Find a and b.
~~~~~~~~~~~~~~~~~
Let me to denote / (to call) f(x) = 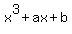 .
The condition says that
f(x) = g(x)*(x^2-1) + (x+2), where g(x) is some polynomial of degree 1, but its exact expression does not matter for me now.
It is the exact meaning of this statement "The remainder of x^3+ax+b when divided by (x^2-1) is x+2".
Now, if x = 1, then
f(1) = g(1)*(1^2-1) + (1+2) = g(1)*0 + 3 = 3. (1)
If x = -1, then
f(-1) = g(-1)*((-1)^2-1) + (-1+2) = g(-1)*0 + 1 = 1. (2)
In other words, using the explicit form of f(x), the equation (1) takes the form
.
The condition says that
f(x) = g(x)*(x^2-1) + (x+2), where g(x) is some polynomial of degree 1, but its exact expression does not matter for me now.
It is the exact meaning of this statement "The remainder of x^3+ax+b when divided by (x^2-1) is x+2".
Now, if x = 1, then
f(1) = g(1)*(1^2-1) + (1+2) = g(1)*0 + 3 = 3. (1)
If x = -1, then
f(-1) = g(-1)*((-1)^2-1) + (-1+2) = g(-1)*0 + 1 = 1. (2)
In other words, using the explicit form of f(x), the equation (1) takes the form
 = 3, or 1 + a + b = 3, or simply a + b = 2. (3)
Using the explicit form of f(x), the equation (2) takes the form
= 3, or 1 + a + b = 3, or simply a + b = 2. (3)
Using the explicit form of f(x), the equation (2) takes the form
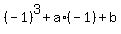 = 1, or -1 - a + b = 1, or simply -a + b = 2. (4)
Thus you got these two equations
a + b = 2, (5)
a - b = 2. (6)
Add them (both sides), and you will get 2a = 4; hence, a = 2.
Then from (5), b = 2 - a = 2 - 2 = 0.
Answer. a = 2, b = 0.
= 1, or -1 - a + b = 1, or simply -a + b = 2. (4)
Thus you got these two equations
a + b = 2, (5)
a - b = 2. (6)
Add them (both sides), and you will get 2a = 4; hence, a = 2.
Then from (5), b = 2 - a = 2 - 2 = 0.
Answer. a = 2, b = 0.
Solved.