|
Question 1086403: what is the equation of the line bisector of the acute angle formed by the intersection of the lines 4x+3y-24=0 and 5x-12y+30=0
Answer by KMST(5328)   (Show Source): (Show Source):
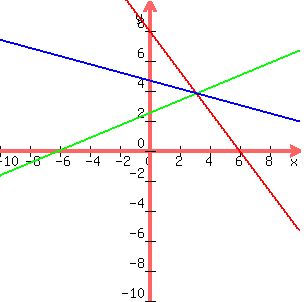
You can put this solution on YOUR website!  shows shows  and and  lines. lines.
Those lines form four angles.
Because those line are are not perpendicular to each other,
two of those angles are acute and two are obtuse.
The bisector of an angle is the locus of the points that are
at equal distance from the two sides of the angle.
Distance from a point 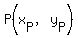 to a line to a line  is is
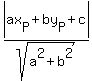 . .
So, the lines bisecting the angles formed by  and and 
have the equations
  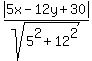 . .
That simplifies to
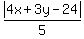   , ,
and to
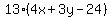  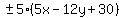
and
   . .
The plus sign would give us
 <--> <-->  <--> <-->  <--> <-->  , ,
with a slope of 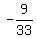  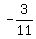 , ,
showing a slight downward slope.
The minus sign would give us
 <--> <-->  <--> <-->  , ,
with a slope of 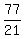  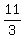 , ,
showing a very steep upwards slope.
The line  has a shallow upwards slope of has a shallow upwards slope of 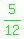 . .
The line  has a slope of has a slope of 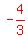 (downwards). (downwards).
A line perpendicular to  would have a steeper upwards slope of would have a steeper upwards slope of
 . .
So, the acute angle between  and and 
includes shallower slopes between 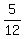 and and  , ,
such as 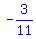 , not steeper slopes, such as , not steeper slopes, such as  or or 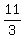 . .
That means that the acute angle bisector line is

|
|
|
| |